Benchmarks & Goodhart’s Law
Make sure you understand your workload. Putting your faith in benchmark results may lead you astray.

“When a measure becomes a target, it ceases to be a good measure" - Goodhart's Law
I believe this applies to software benchmarks as much as the monetary theory that Charles Goodhart originally coined (pun intended) it for in 1975.
Let me explain. Once upon a time someone came up with a good way to measure the performance of a processor. The way this was done was probably relevant to that person’s use case or understanding of what exactly needed to be measured. Let’s even pretend for now that this aligns with what you need to measure. It probably doesn’t but that’s a topic for another day.
This lovely benchmark becomes a popular way of comparing processors and its output starts to feed into purchasing decisions. Naturally the processor manufacturers take note and ensure that newer processors perform better on this benchmark. That’s good right? Right?
Maybe. It’s good for only if whatever was done to improve the performance of the benchmark also improves the performance of your code.
It’s also not unheard of for a processor manufacturer to tweak the benchmark itself (which may be perfectly fair) but again, this is only helpful if you’re able to make similar modifications to your own code and know that you need to.
Rinse and repeat multiple times and you’d better be sure that the benchmarks numbers have a meaningful correlation to the performance of your own software. This is especially true if you start comparing large numbers and varieties of processors such as, oh I don’t know, everything you could rent in the cloud.
This certainly isn’t a theoretical problem either. This graph shows, on the y axis, the scores of Passmark CPU a popular CPU benchmark and COREx a financial risk system benchmark. The x axis is simply VM types ordered by increasing Passmark score (higher scores are better). The results are for 64 vCPU machines available on AWS, Azure and GCP and include a total of 63 different VM types.
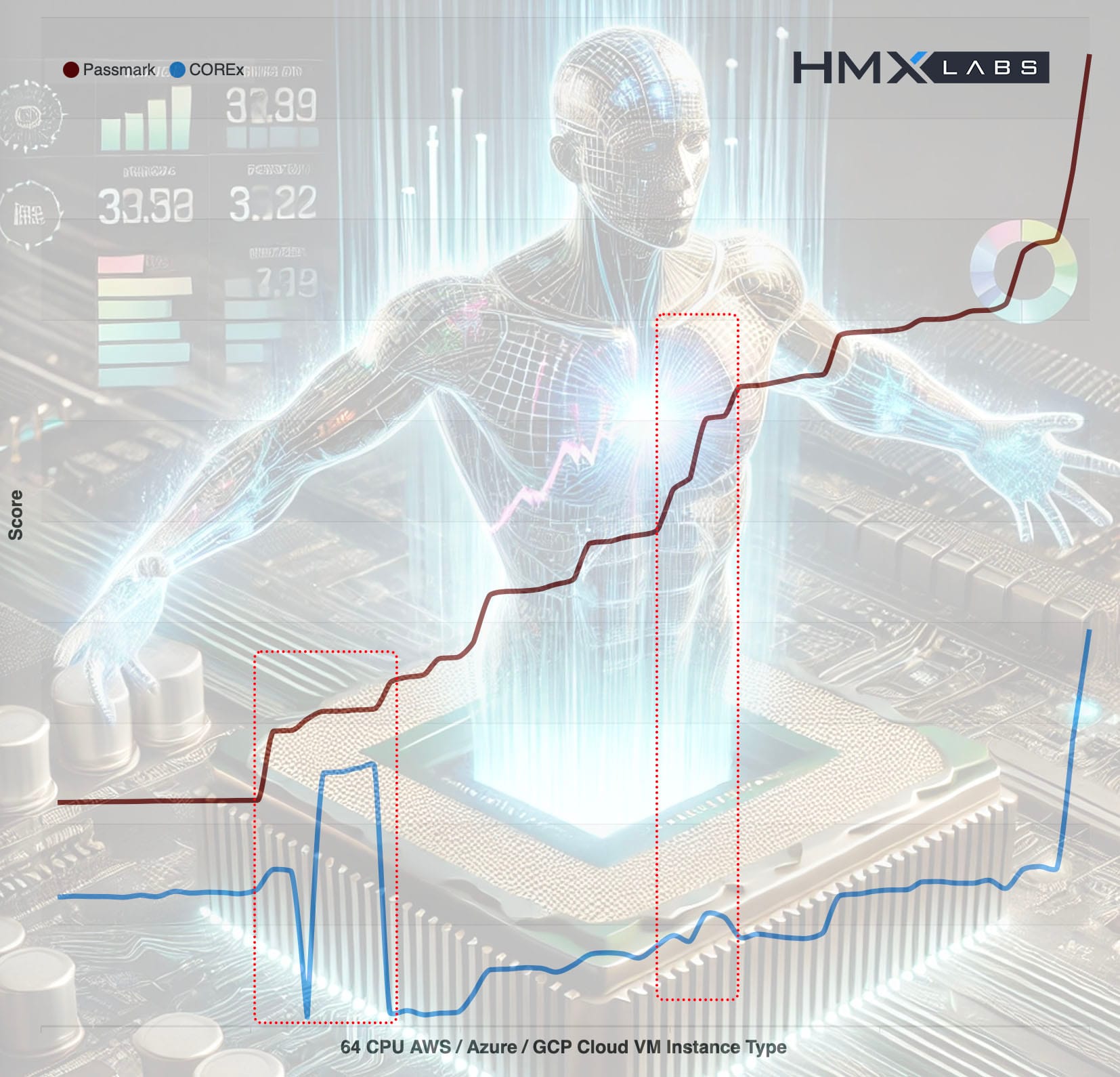
Financial risk analytics is a highly CPU bound problem. There should be a strong correlation here, and there is. Except when there isn’t. While the lines mostly correlate there are some interesting deviations highlighted in red.
The moral of the story is to pick your benchmarks carefully, or better still, don’t use a synthetic benchmark at all. Wrap up a representative sample of your own workload and compare that.




